The strange nature of this problem has earned it the name
What is the maximum number of steps a 2-symbol ({0,1}), n-state Turing Machine can take, starting from an initially zeroed-out tape, before halting? The function that gives this value for a given number of states n - BB(n) - is called the Busy Beaver (maximum shift) function.
Obtaining each value requires proving the behavior of all programs with that number of states - whether they run indefinitely or halt - and if so, after how many steps.
The highest number of steps for 5-state machines was recently proven to be 47,176,870, and with this all values of BB(n) up to BB(5) are now known. Now, work has begun to find the longest running (but halting) Turing Machine program with 6 states - the value of BB(6).
But researchers have already encountered a difficult problem: a 6-state machine that exhibits behavior of a kind no one has ever managed to prove to halt or not. Its behavior is simple:
Starting with the number 8, and repeatedly adding half of the number to itself, rounding down to get a whole number (8->12->18->27->40->60->90->135->202…), will there eventually be a point where you have seen (strictly) more than twice as many odd numbers as even numbers (if so, halt)?
mathematics:
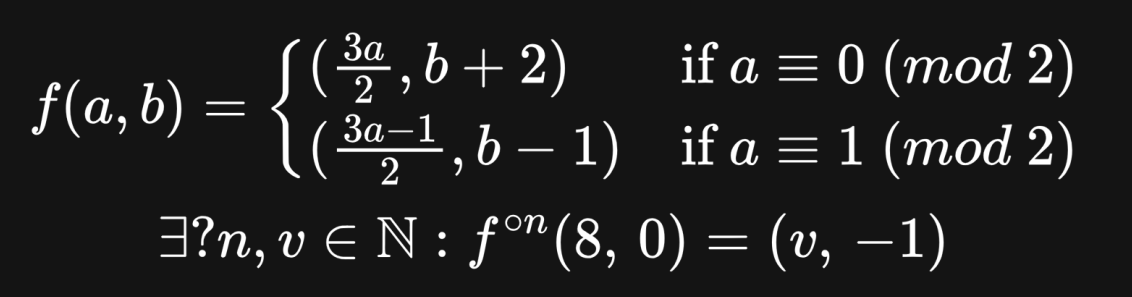
# Does this Python function halt?
def antihydra():
a = 8
b = 0
while b != -1:
if a % 2 == 0:
b += 2
else:
b -= 1
a += a//2(with numbers not overflowing, and // denoting integer division, which in this case is equivalent to one bit shift to the right >> 1)
but even attempts at a proof have been elusive.
By probabilistic argument it seems likely that it will never halt. But nonetheless it might, and if so, might even be the longest running program and thus determine the value of BB(6). So it is necessary to understand its behavior in order to conclusively prove the value of BB(6).
Antihydra is the smallest open problem in mathematics, on the Busy Beaver scale.
It’s Collatz-likeness seems to indicate that…
